COMMON CORE MATH ACTIVITIES
Meeting the Needs of ALL Students!
Free Sample Common Core Math Activity Sheets
Common Core Math Activities (CCMA) include an elementary math curriculum that is 100 percent aligned to the Common Core Math Standards, and CCMA offers the flexibility of using worksheets for independent practice and interactive activity sheets as guided practice. Many educators trust Common Core Math Activities to undeniably support the teaching and learning of students of all levels of proficiency. Try out vast assortment of activities, worksheets, and activity sheets and make math a fun and engaging learning experience.
Select a grade level to view our FREE ACTIVITY SHEETS. You can DOWNLOAD, PRINT, and use them to assess their effectiveness with your students!
Shop our books below!
- All
- 1st Grade
- 2nd Grade
- 3rd Grade
- 4th Grade
- 5th Grade

7 Strategies- Master Basic Addition Facts

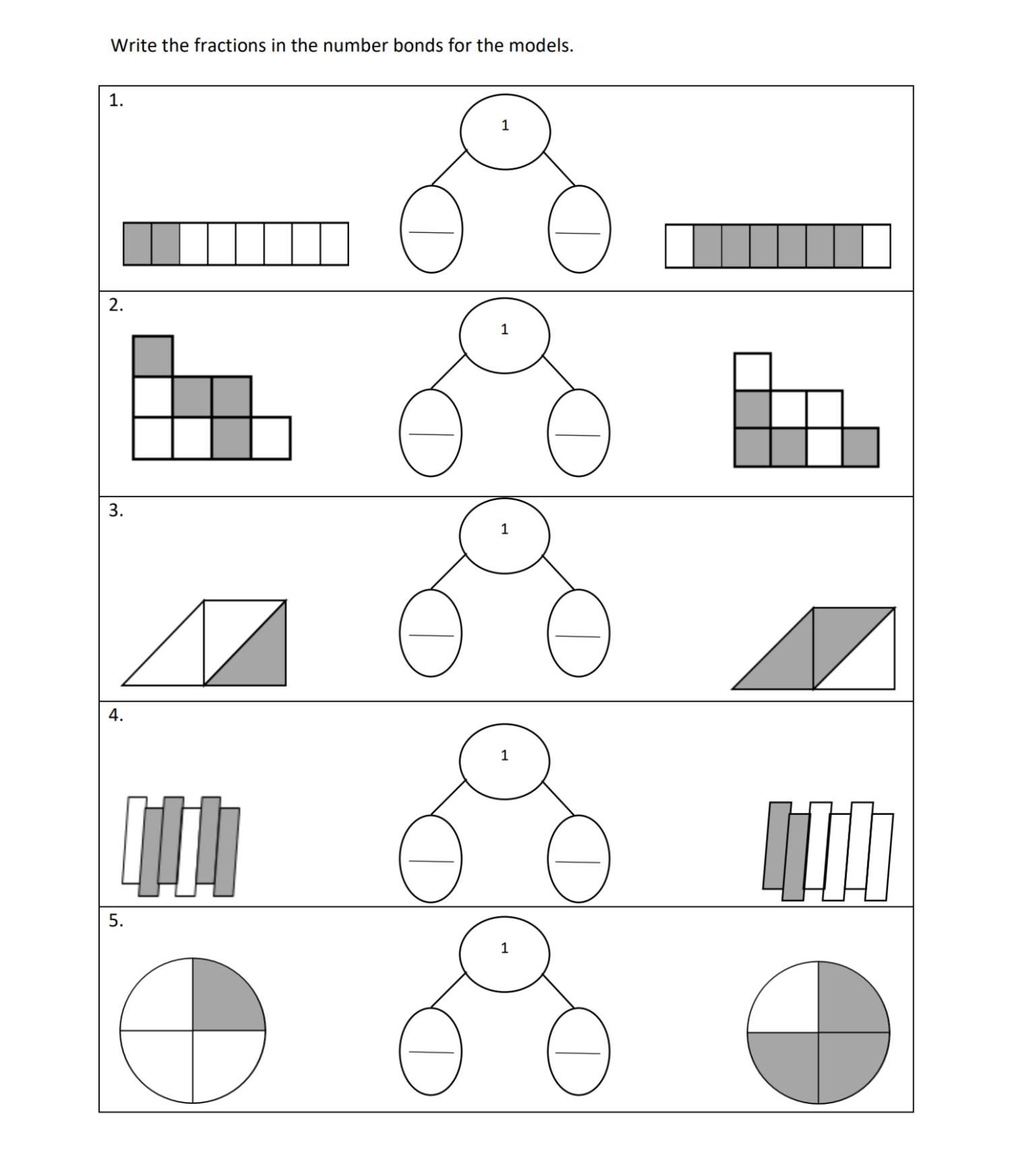
1st Grade, Activity 426: Reason with Shapes and their Attributes
Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of.
Describe the whole as two of, or four of the shares. Understand for these examples that decomposing into more equal shares creates smaller shares.
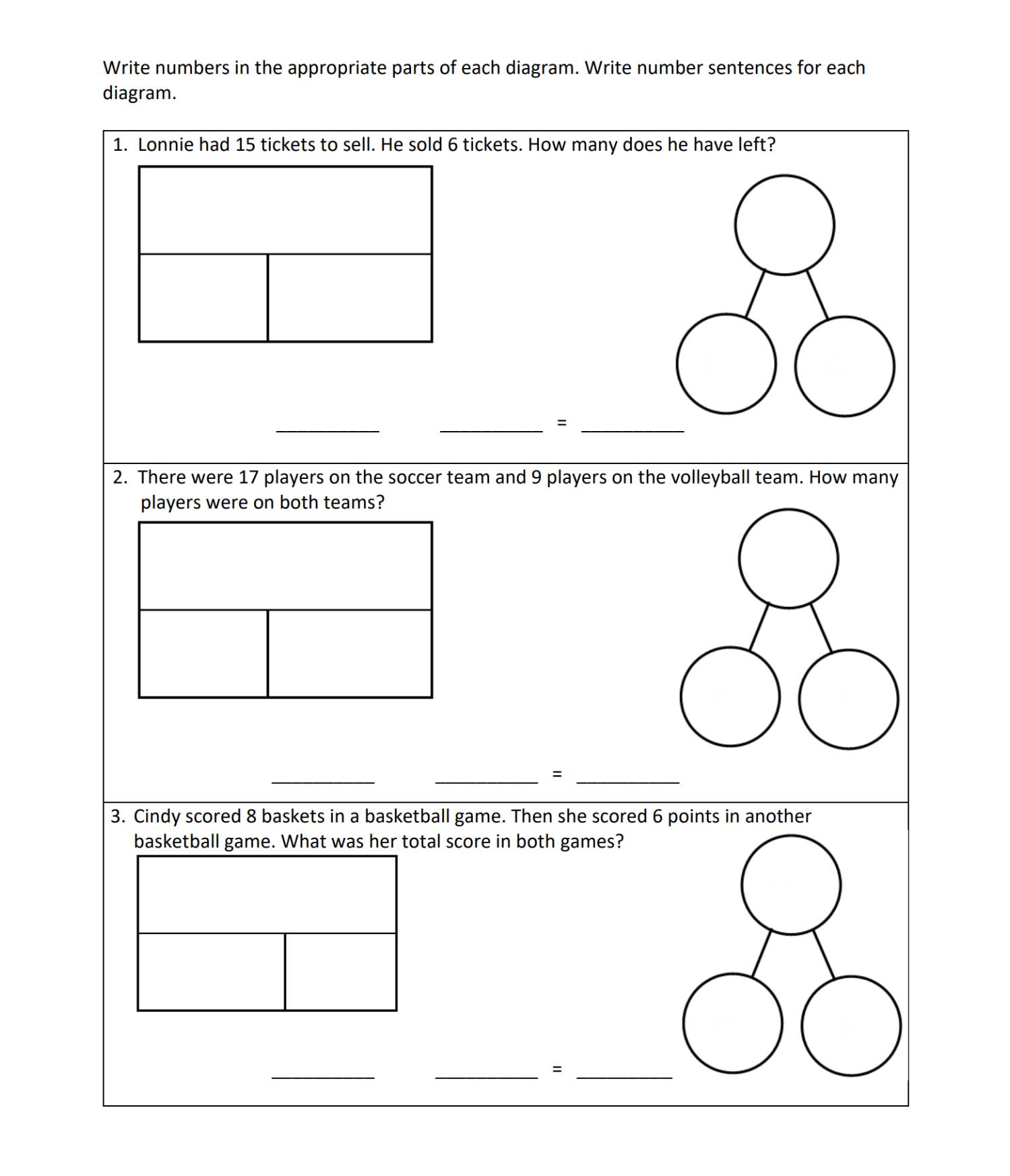
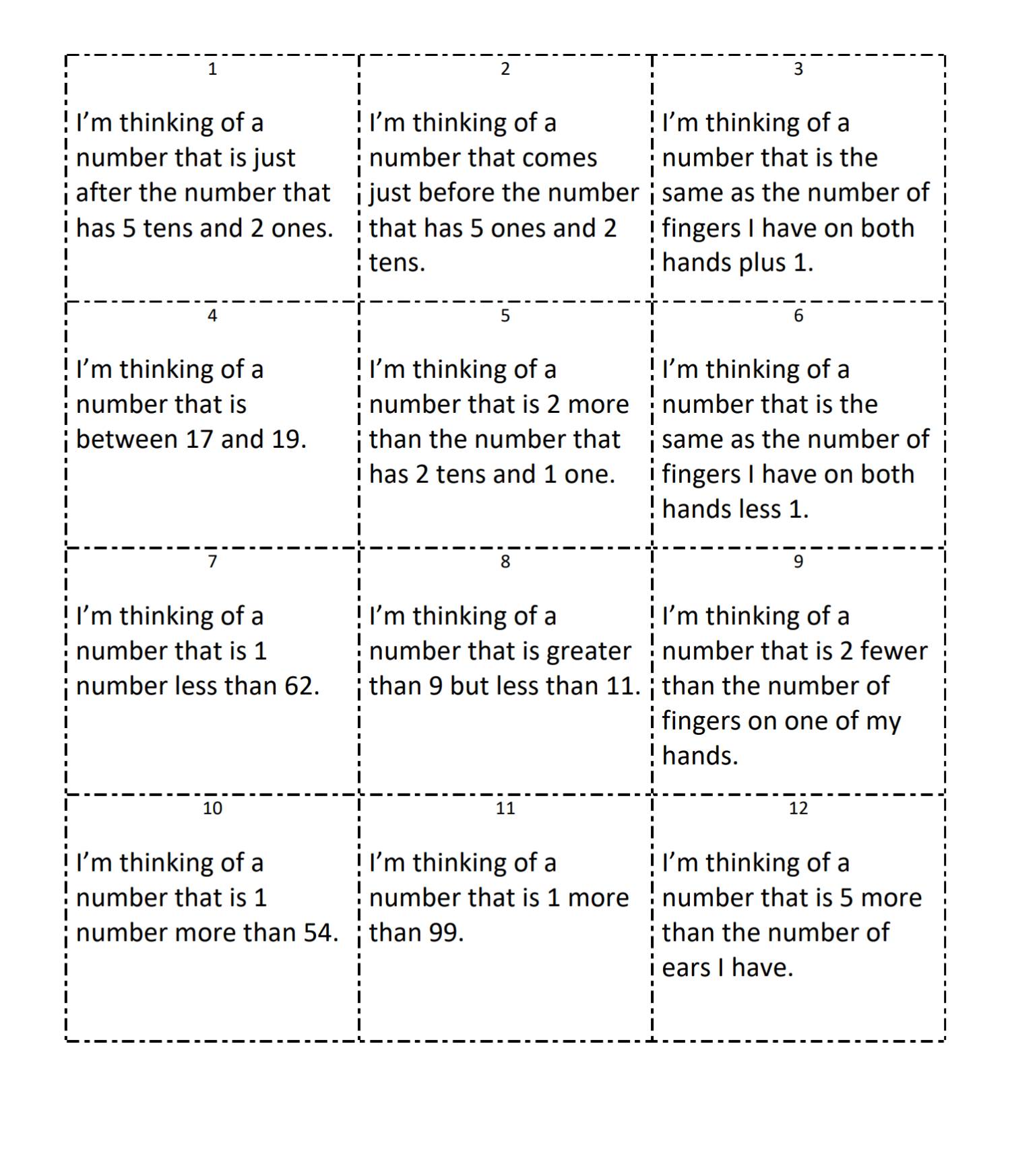
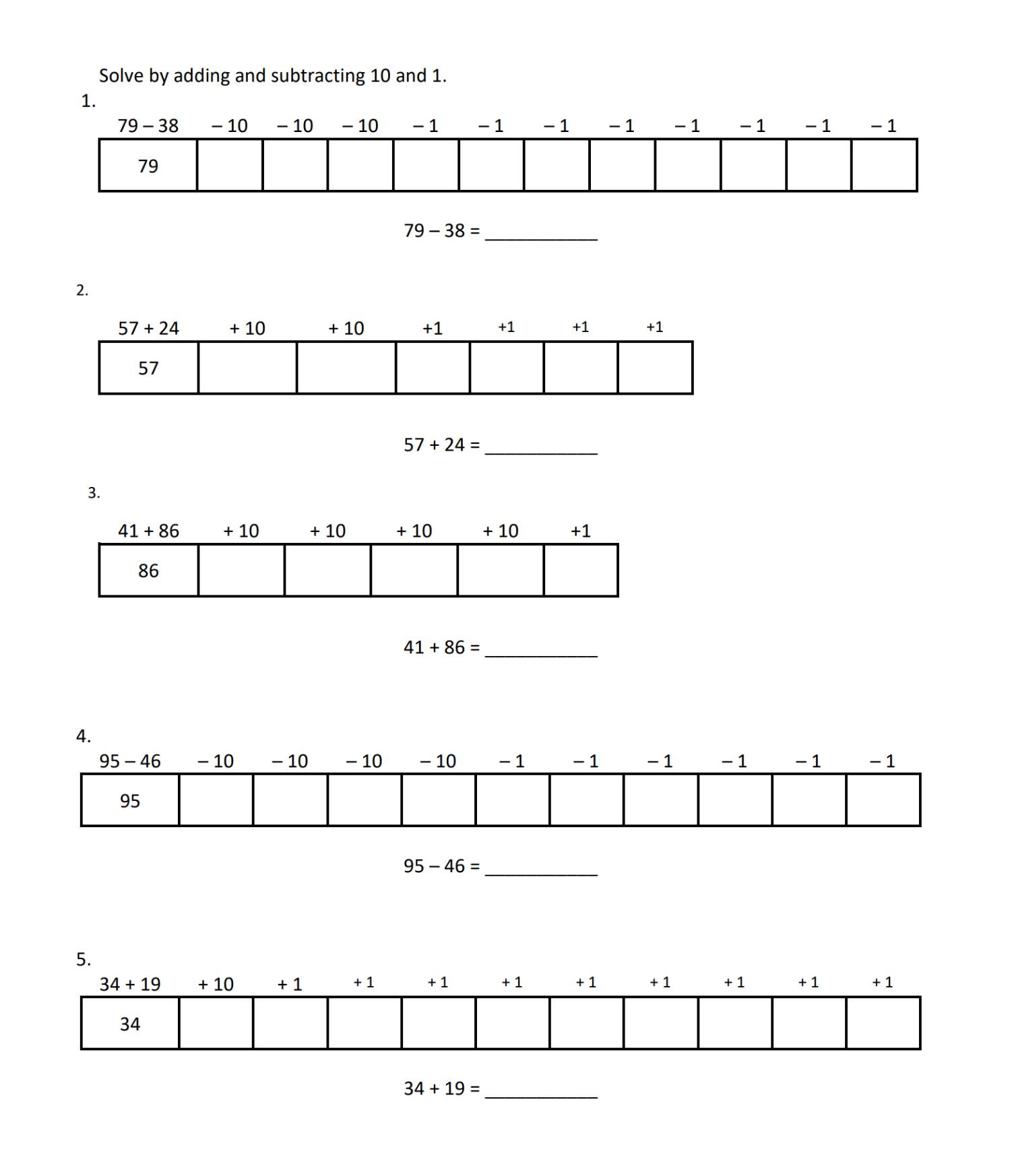
2nd Grade, Activity 13: Represent and Solve Problems Involving Addition and Subtraction
Use addition and subtraction within 100 to solve one-and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
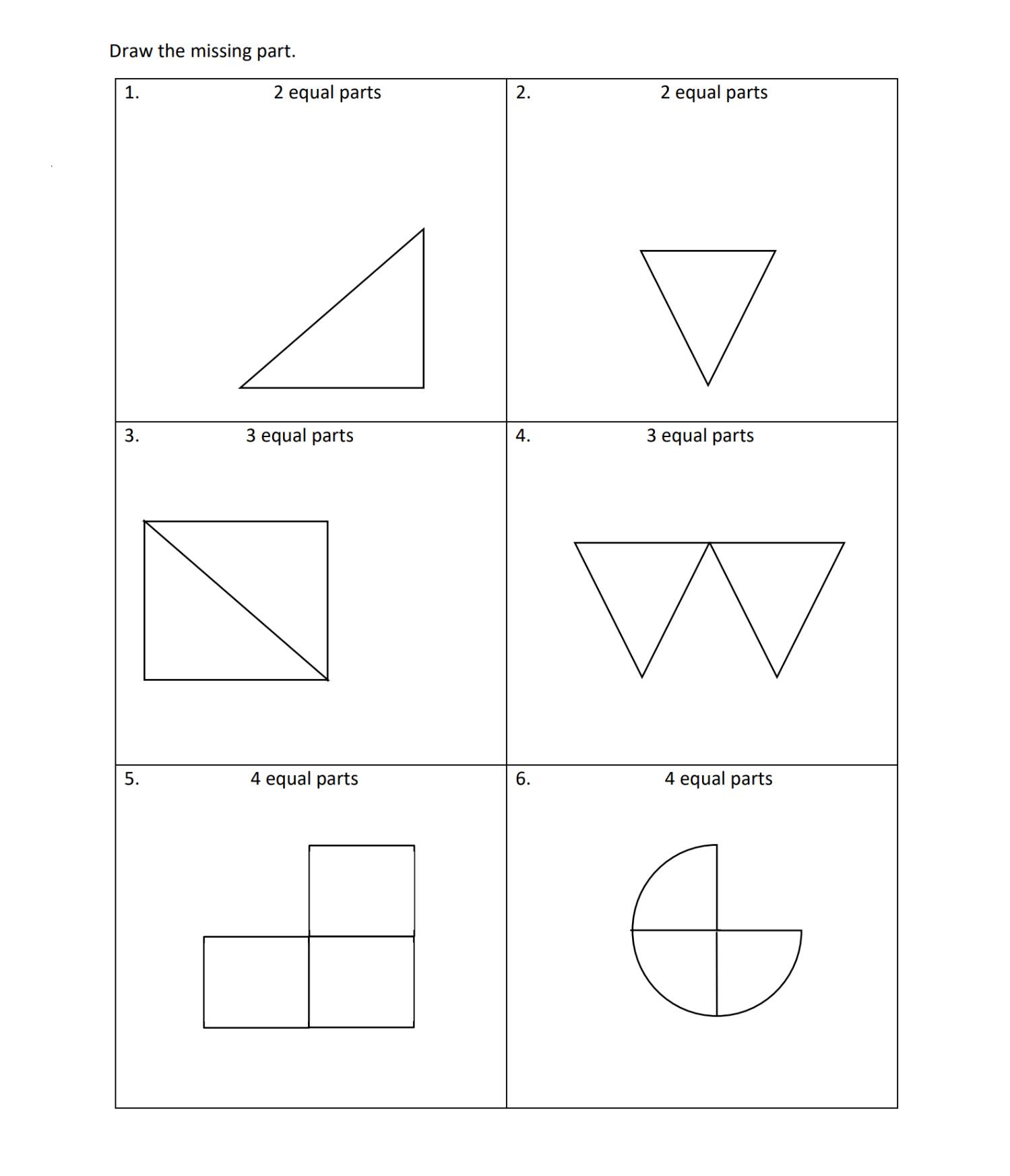
2nd Grade, Activity 376: Reason with Shapes and their Attributes
Partition circles and rectangles into two, three, or four equal shares, describe the shares using the words halves, thirds, half of, a third of, etc., and describe the whole as two halves, three thirds, four fourths. Recognize that equal shares of identical wholes need not have the same shape.
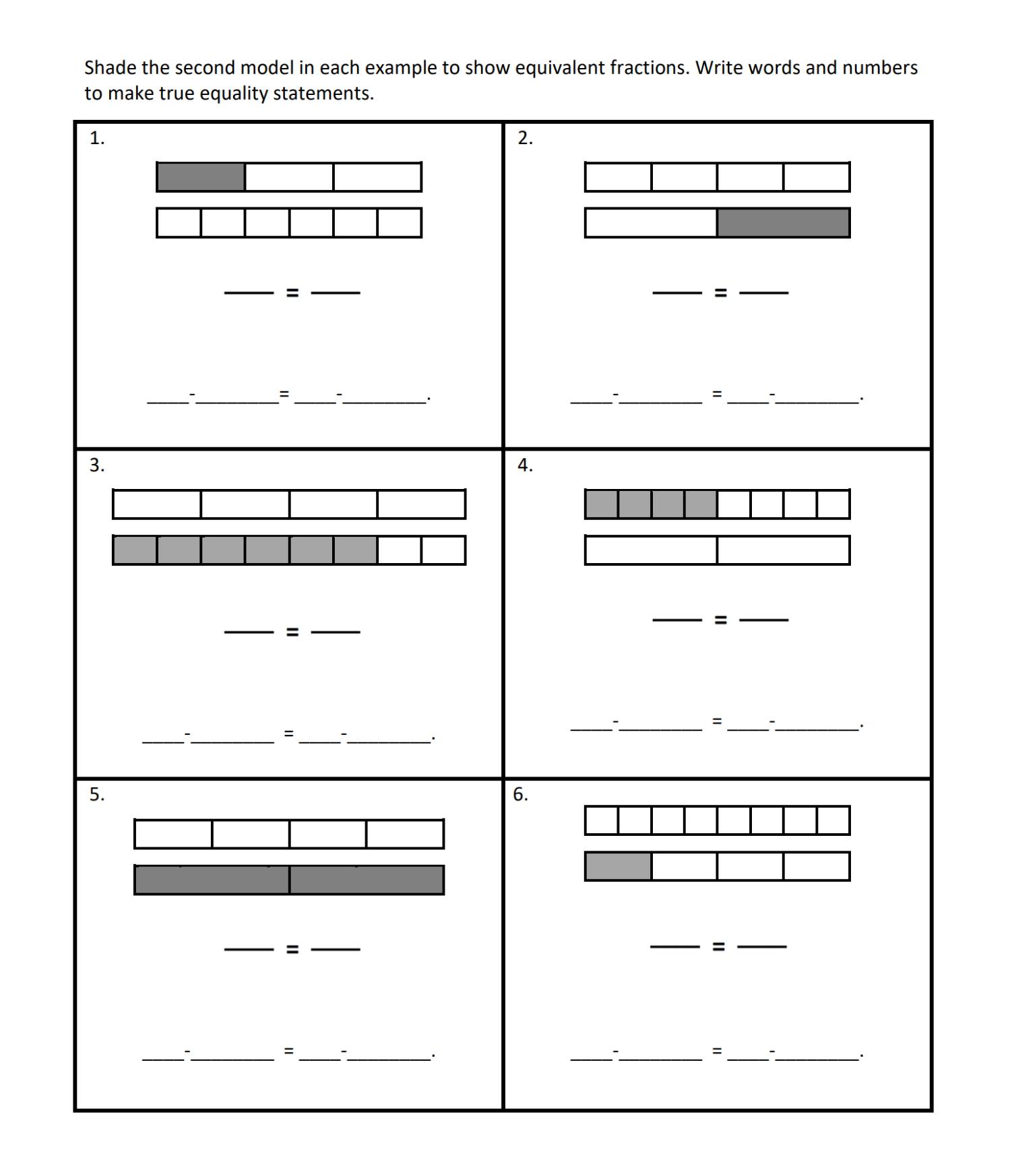
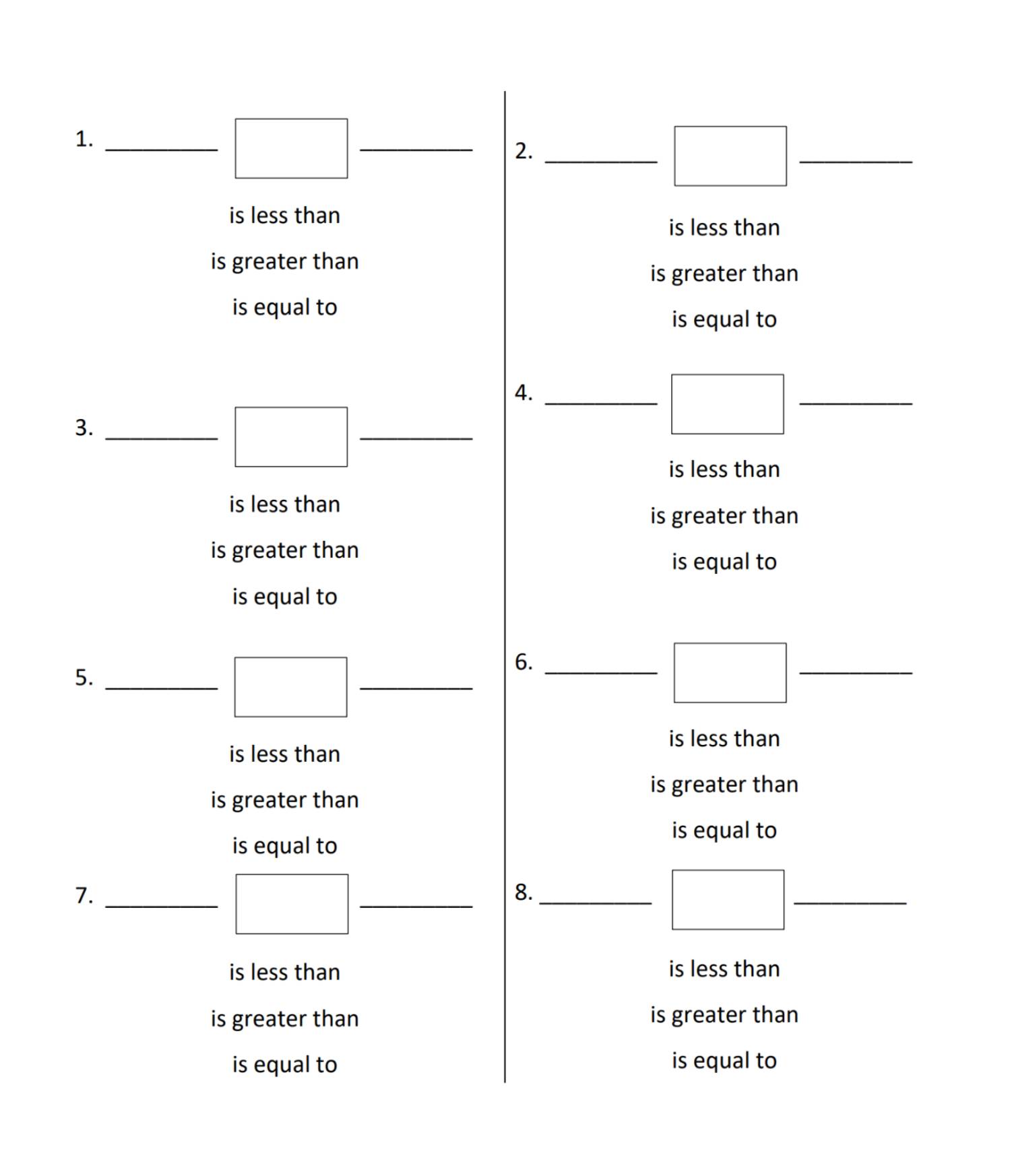
3rd Grade, Activity 258: Develop Understanding of Fractions as Numbers
Explain equivalence of fractions with denominators 2, 3, 4, 6, and 8 in special cases, and compare fractions by reasoning about their size.
b. Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
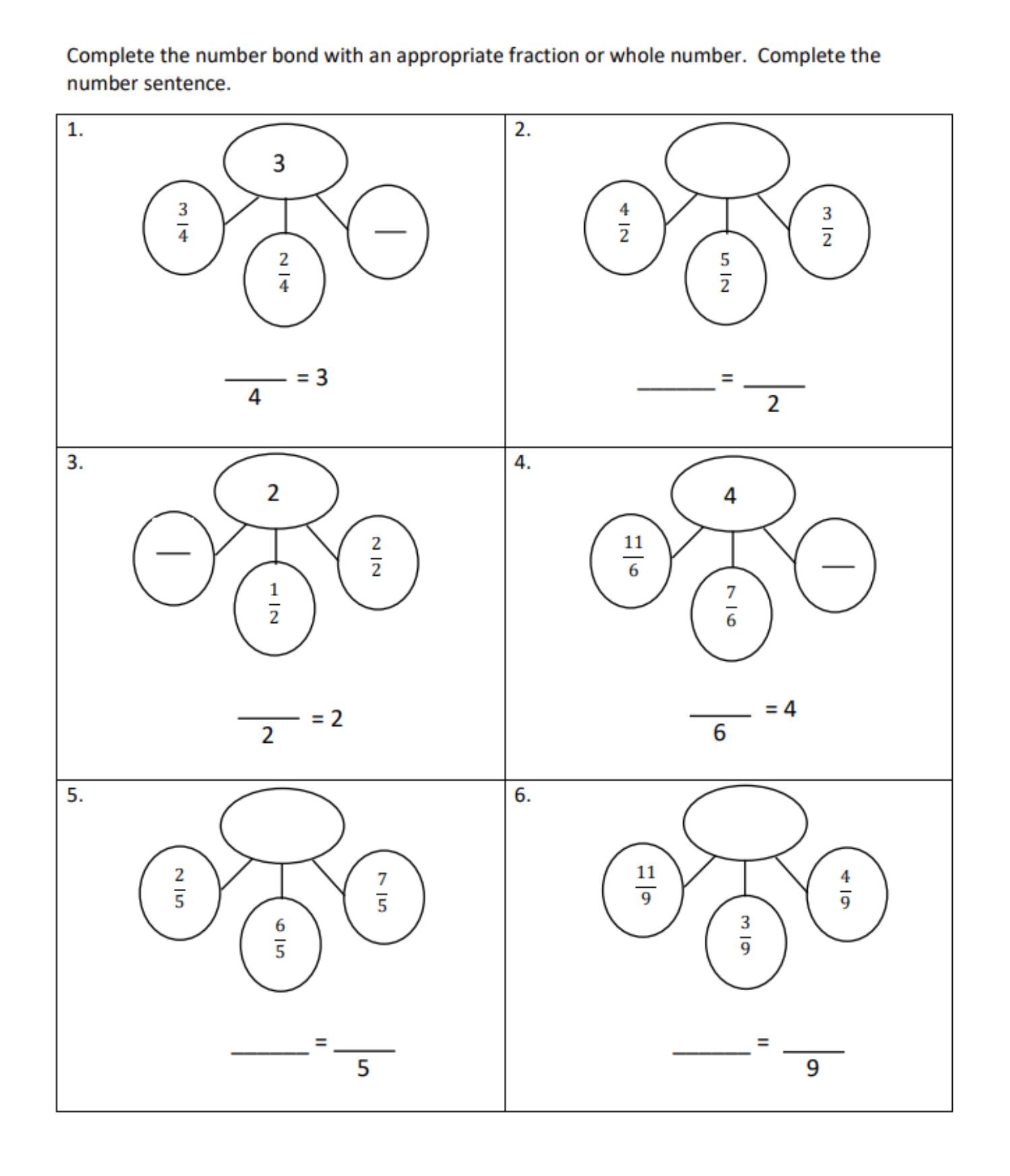
3rd Grade, Activity 270: Develop Understanding of Fractions as Numbers
Explain equivalence of fractions with denominators 2, 3, 4, 6, and 8 in special cases, and compare fractions by reasoning about their size.
c. Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
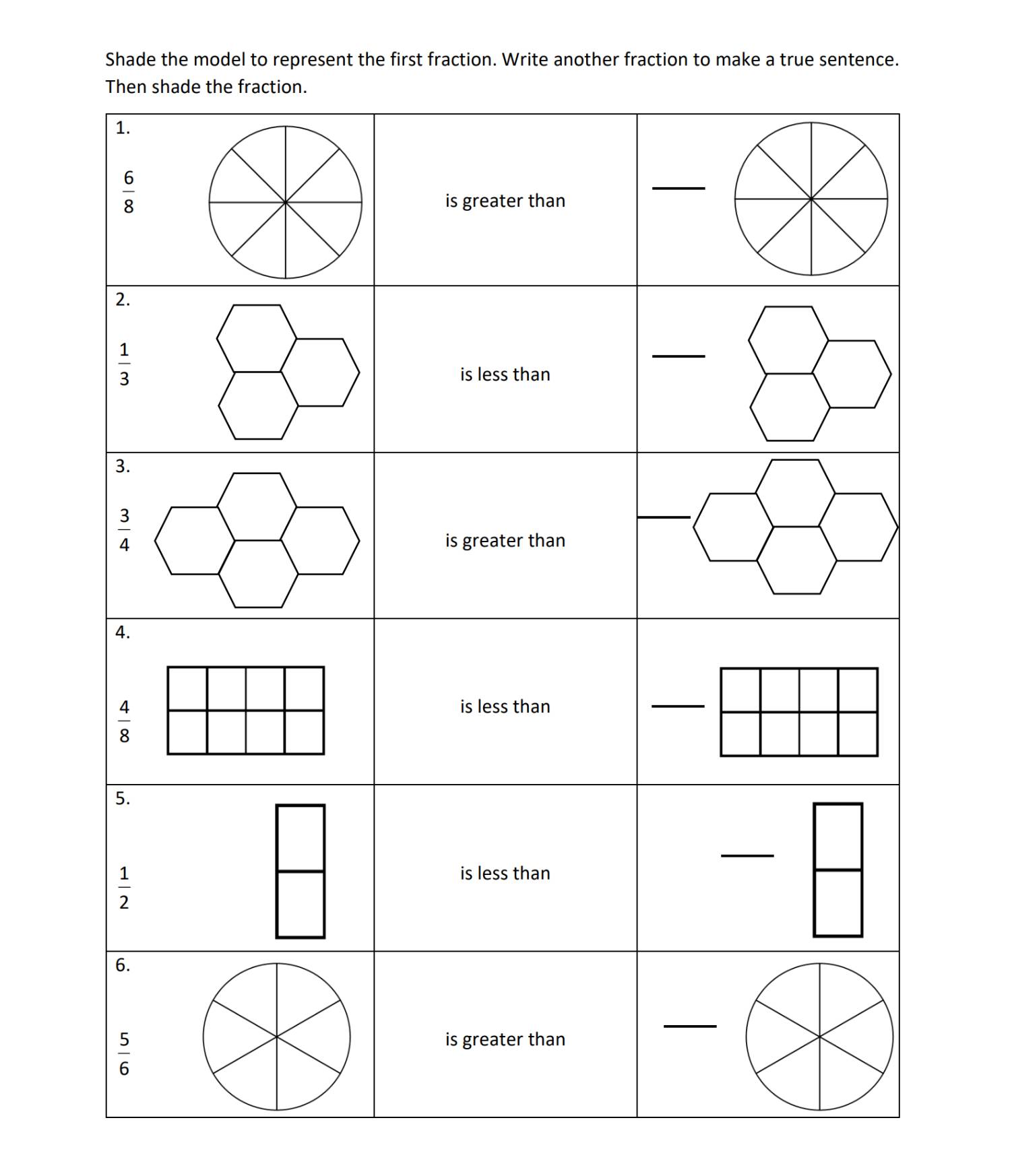
3rd Grade, Activity 277: Develop Understanding of Fractions as Numbers
Explain equivalence of fractions with denominators 2, 3, 4, 6, and 8 in special cases, and compare fractions by reasoning about their size.
d. Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.

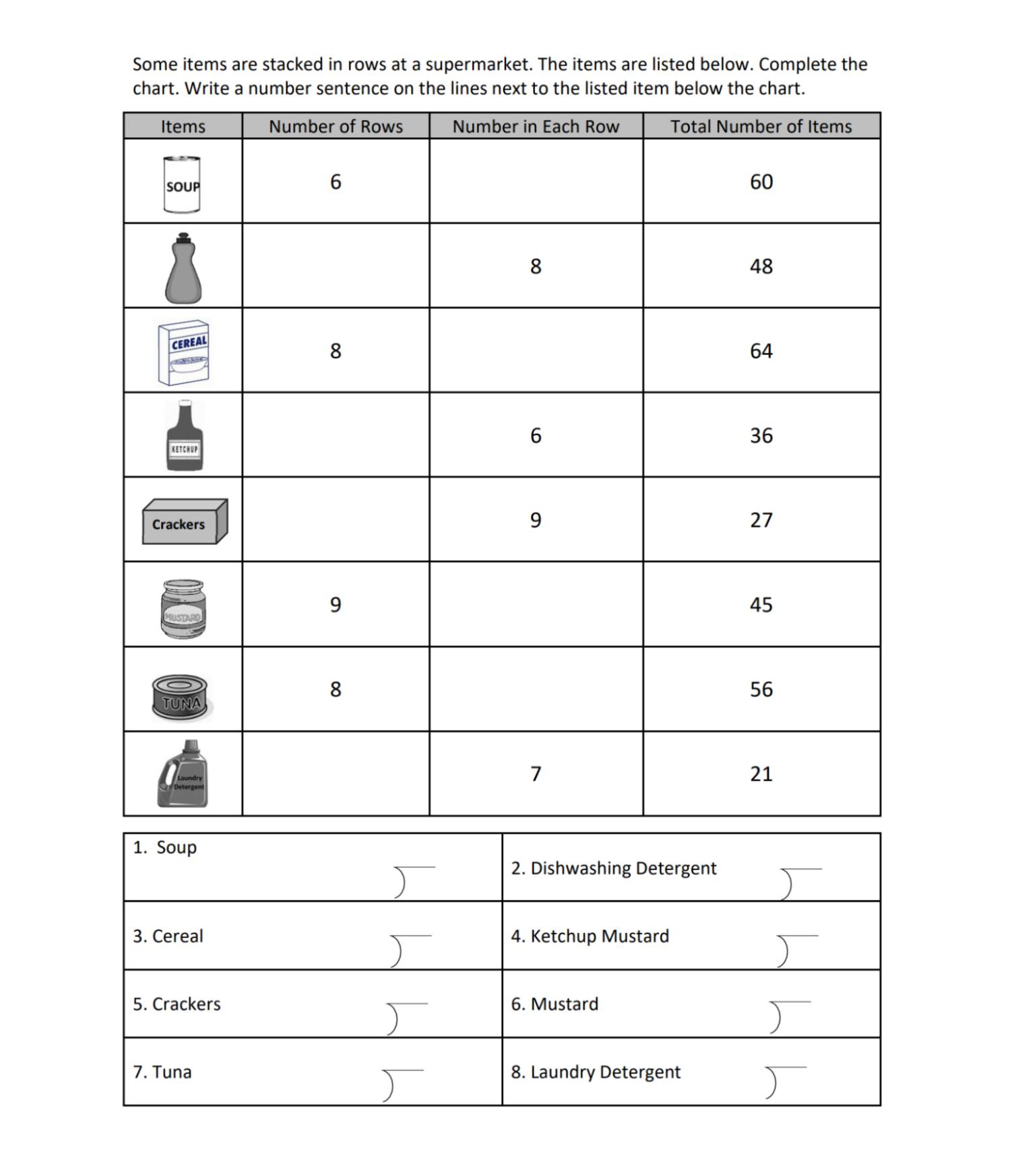
3rd Grade, Activity 339: Represent and Interpret Data
Draw a scaled picture graph and a scaled bar graph to represent a data set with several categories. Solve one- and two-step “how many more” and “how many less” problems using information presented in scaled bar graphs. For example, draw a bar graph in which each square in the bar graph might represent 5 pets.

4th Grade, Activity 3: Use the Four Operations with Whole Numbers to Solve Problems
Interpret a multiplication equation as a comparison and represent verbal statements of multiplicative comparisons as multiplication equations, e.g., interpret 35 = 5 x 7 as a statement that 35 is 5 times as many as 7, and 7 times as many as 5.

4th Grade, Activity 54: Use the Four Operations with Whole Numbers to Solve Problems
Solve multi-step word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.

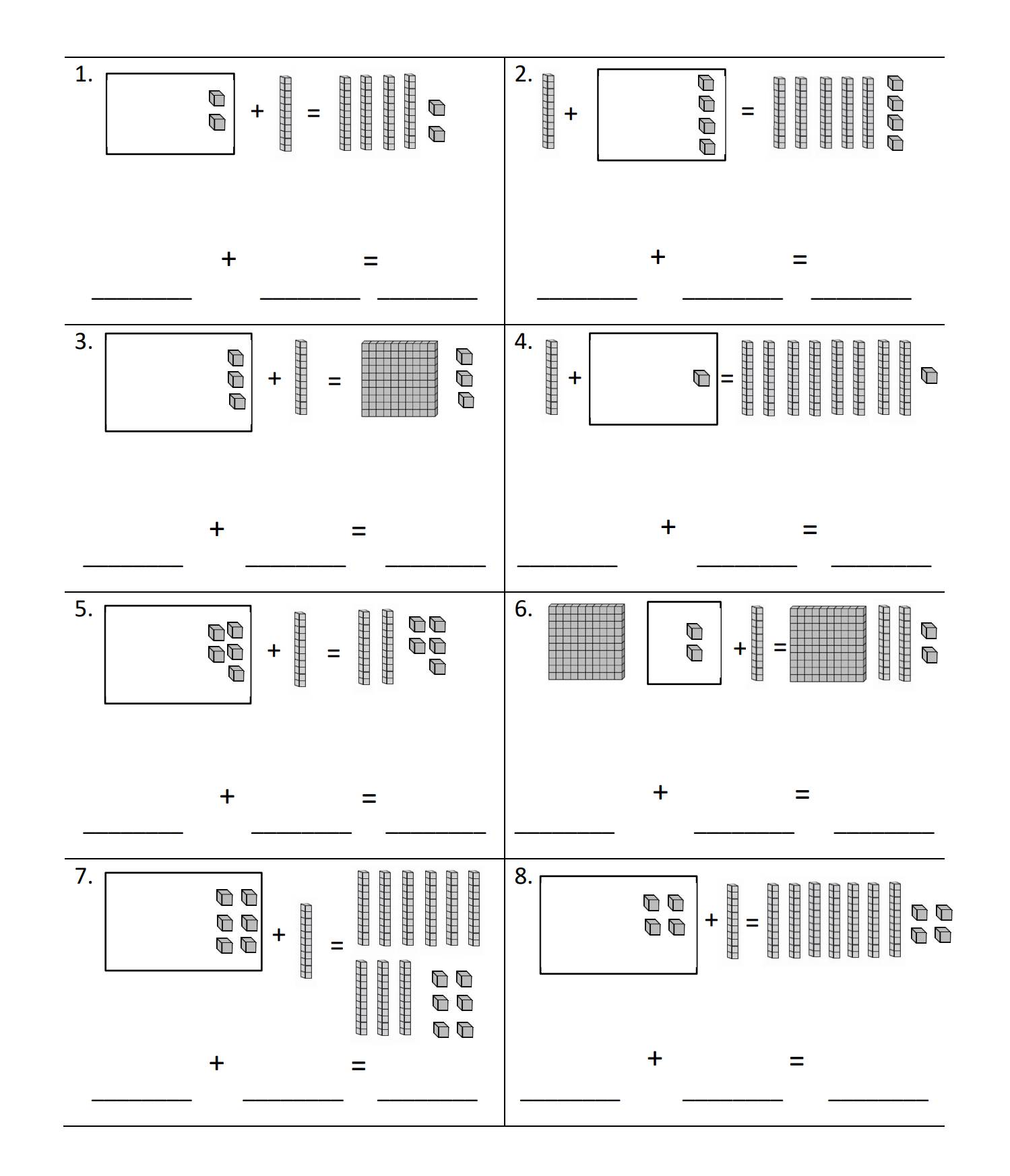
4th Grade, Activity 237: Build Fractions from Unit Fractions by Applying and Extending Previous Understandings of Operations on Whole Numbers
Understand a fraction a/b with a > 1 as a sum of fractions 1/b. (Denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, and 100.)
a. Understand addition and subtraction of fractions as joining and separating parts referring to the same whole. Example: 3/4 = 1/4 + 1/4 + 1/4

4th Grade, Activity 386: Solve Problems Involving Measurement and Conversion of Measurements from a Larger Unit to a Smaller Unit
Apply the area and perimeter formulas for rectangles in real-world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.

4th Grade, Activity 419: Geometric Measurement: Understand Concepts of Angle and Measure Angles
Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement:
c. An angle that turns through n one-degree angles is said to have an angle measure of n degrees.

5th Grade, Activity 16: Write and Interpret Numerical Expressions
Write simple expressions that record calculations with whole numbers, fractions, and decimals, and interpret numerical expressions without evaluating them.
For example, express the calculation “add and 7, then multiply by 2” as 2 × (8 + 7). Recognize that 3 x (18,932 + 9.21) is three times as large as 18,932 + 9.21, without having to calculate the indicated sum or product.

5th Grade, Activity 171: Use Equivalent Fractions as a Strategy to Add and Subtract Fractions
Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators.
For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (In general, a/b + c/d = (ad + bc)/bd.)

5th Grade, Activity 217: Apply and Extend Previous Understandings of Multiplication and Division to Multiply and Divide Fractions
Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b). Solve word problems involving division of whole numbers leading to answers in the form of fractions or mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
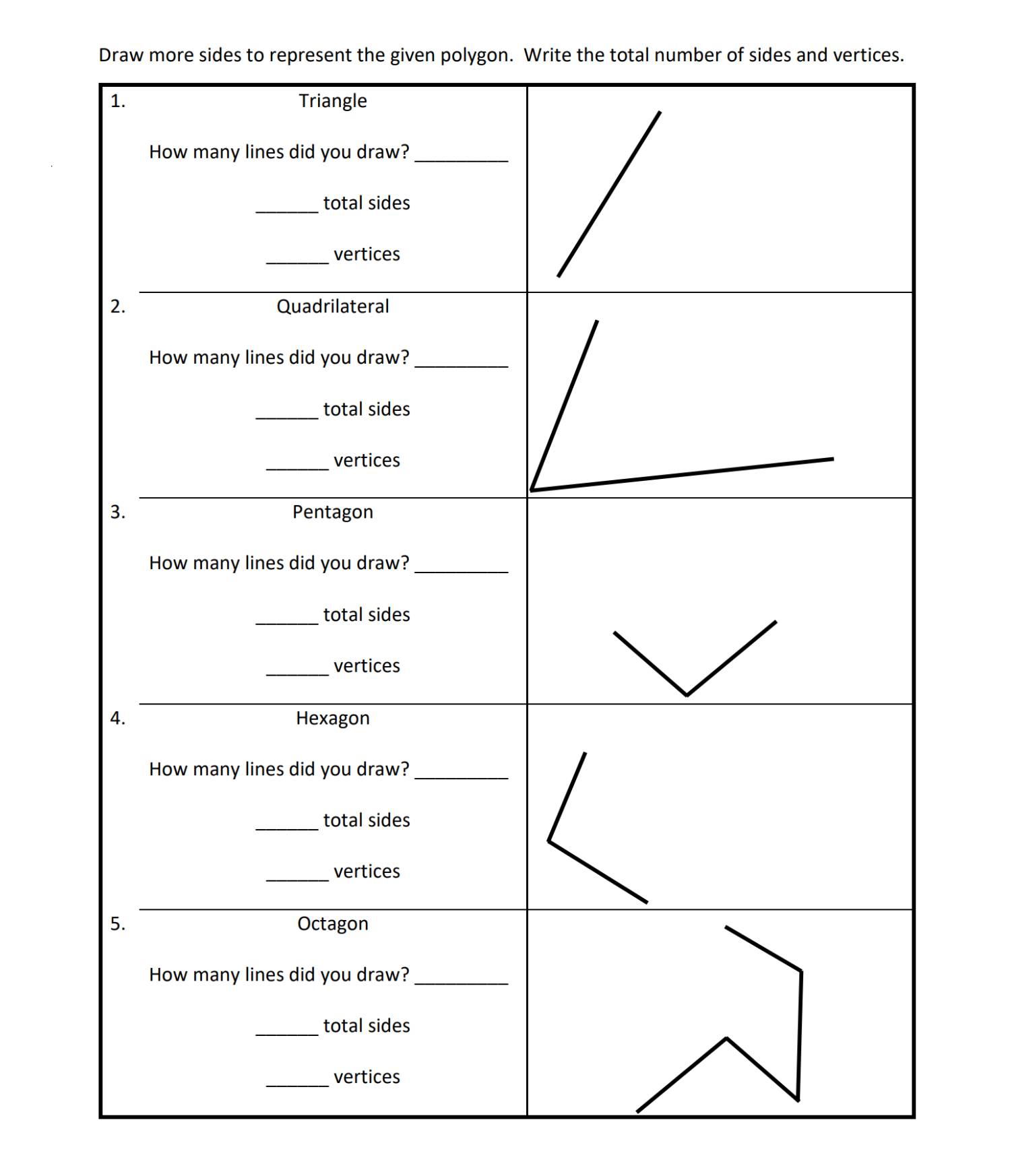
5th Grade, Activity 343: Classify Two-Dimensional Figures into Categories Based on their Properties
Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category.
For example, all rectangles have four right angles and squares are rectangles, so all squares have four right angles.