COMMON CORE MATH ACTIVITIES
Meeting the Needs of ALL Students!
3rd Grade, Activity 258: Develop Understanding of Fractions as Numbers
Explain equivalence of fractions with denominators 2, 3, 4, 6, and 8 in special cases, and compare fractions by reasoning about their size.
b. Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
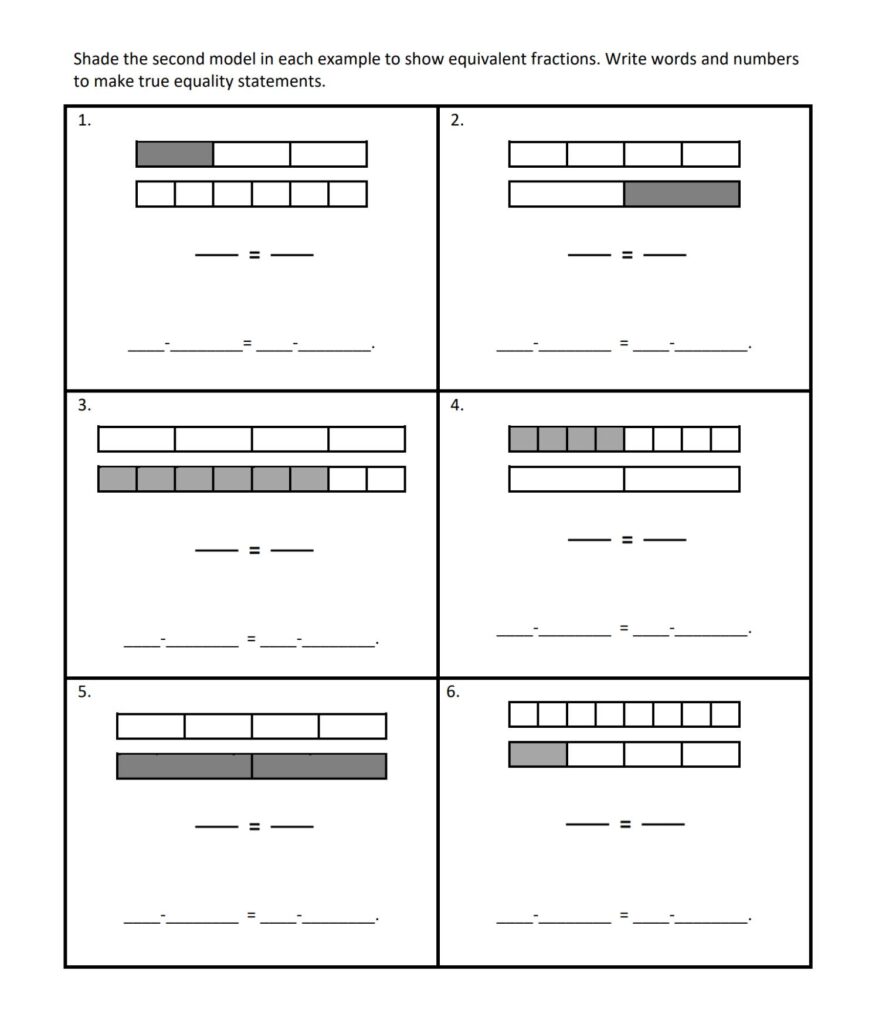
Using Models to Represent Equivalent Fractions
- Group: Whole Group/Alone
- Materials: Using Models to Represent Equivalent Fractions sheet, map pencils
Issue the Using Models to Represent Equivalent Fractions sheet and map pencils to each student. Lead students through the first problem on the sheet. Discuss the number of parts on each model and emphasize that both models are the same length. Have students state the parts as thirds and sixths. Direct students to shade one part of the thirds model as directed on the sheet.
- Ask: What fraction of the thirds model is shaded? (one-third)
Instruct students to write the fraction 1⁄3. - Ask: How many parts on the sixths model can be shaded to have the exact same length as one-third? (2)
Instruct students to shade 2-sixths of the sixths model. Have them write the fraction 2⁄6. Instruct them to write the
fraction equality statement and the verbal equality statement underneath the two models.
1⁄3 = 2⁄6
One-third is equal to 2 sixths or 2 sixths is equal to one-third.
Ask questions to check for understanding.
- Are the equal parts the same size?
Guide students through Problem 2 in the same manner. Assign the rest of the problems for students to complete independently, constantly checking for understanding.