COMMON CORE MATH ACTIVITIES
Meeting the Needs of ALL Students!
3rd Grade, Activity 277: Develop Understanding of Fractions as Numbers
Explain equivalence of fractions with denominators 2, 3, 4, 6, and 8 in special cases, and compare fractions by reasoning about their size(Fractions as Numbers).
d. Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
Comparing Fractions
- Group: Alone
- Materials: Comparing Fractions sheet
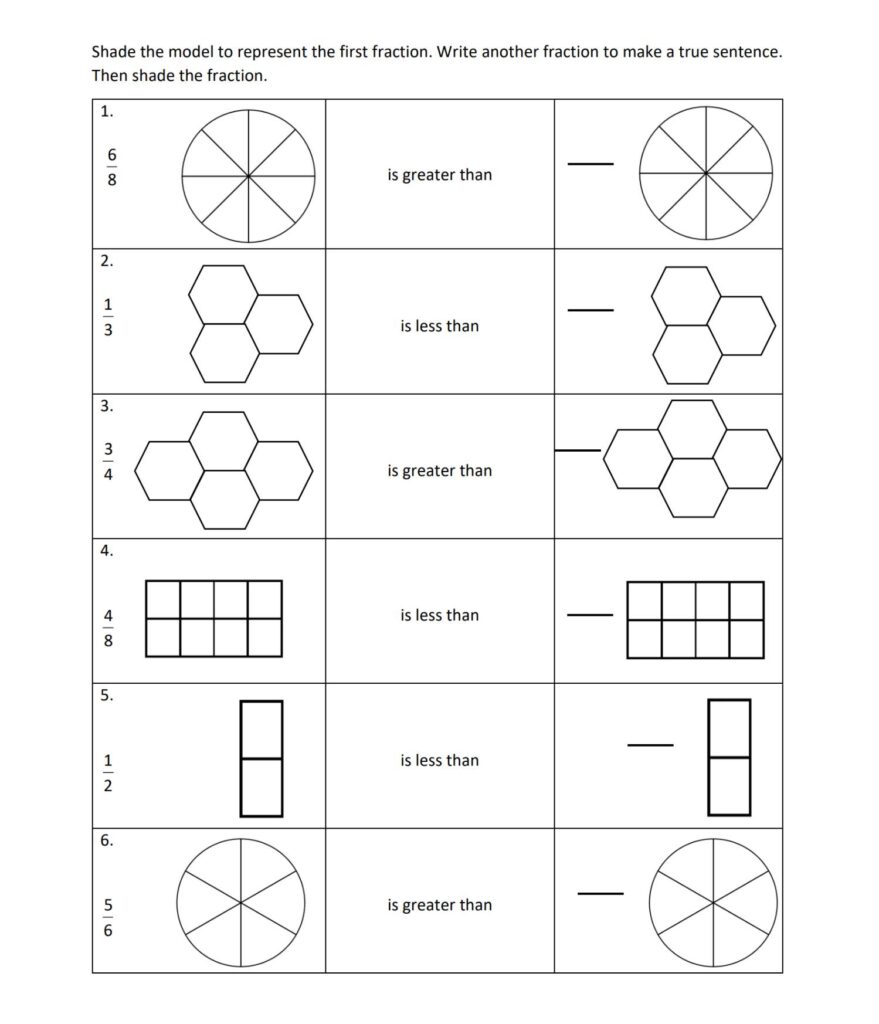
Explain that sometimes it is necessary to compare two fractions to discover which is larger or smaller than the other. Models can be used to decide which fraction is larger or smaller.
Issue a Comparing Fractions sheet to each student. Explain that all model pairs have the same denominator, meaning that the model pairs are divided into the same number of equal parts. Point out that fractions with like denominators have the same number on the bottom number. Have students shade the other fraction model that will make a true sentence. Then direct them to write the fraction. After students complete the sheet, discuss the following questions and emphasize the given points:
- What is the same about each pair of fractions?
- What is different about each pair of fractions?
- If comparing fractions with the same denominator, then the larger the numerator, the larger the fraction.
To conclude, instruct pairs to work together and have each draw three equivalent rectangles and divide them into fourths. They should make sure their rectangles are the same size. Direct students to shade their models to represent a fraction greater than, less than or equal to another student’s fraction. Call on pairs to model their examples on the board.